איפשהו, בשולי המאה ה19, חי מתמטיקאי דגול ולוגיקן מחונן בשם דה מורגן.
יתום מגיל צעיר ועיוור בעינו הימנית, אולם לרגע לא ידע ריפיון או ייאוש.
אדם מוכשר זה, ניסח כללים המונחים בבסיס תורות רבות בנושאים שונים.
בלוגיקה, בתורת הקבוצות, ובאלגברה (בוליאנית).
הכלל האהוב עליי ביותר בכתיב פורמלי, הוא זה:
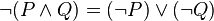
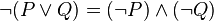
אני הייתי מסבירה את זה ככה:
כללי דה מורגן עוסקים בעצם בניסוח מדוייק של שלילה.
ניקח את הכלל הראשון, שאומר:
השלילה של קיום א' או קיום ב' היא אי קיום א' וגם אי קיום ב'.
במילים פשוטות הייתי מנסחת אותו ככה:
אם מישהו היה שואל אתכם:
"האם היום אתה משחק בכדורגל או בטניס?"
תשובה שלילית מדוייקת תהיה
"היום אני לא משחק בכדורגל וגם לא משחק בטניס"
ואם מישהו מבטיח לך כי
"השיר הזה מדבר עליי וגם עליך"
בשביל להוכיח שאינו דובר אמת עליך להשתמש בכלל השני,
האומר כי:
השלילה של אי קיום א' וגם אי קיום ב', היא אי קיום א' או אי קיום ב'.
כלומר, מספיק לבדוק כי השיר אינו מדבר עליו או אינו מדבר עליך, וכבר אתה מוכיח שדבריו שקר.
לפעמים כללים אלה, מלבד בשפת הדיבור,
מסייעים לנו בתחומים אחרים.
בפסוק לוגי מסוים, אתה יכול לנסח שלילה כ "אין זה נכון ש-"
אבל לפעמים ניתן לנסח את זה באופן מדוייק יותר.
למשל:
"X קטן או שווה לY"
ניתן לומר, בלי להקדיש לזה מחשבה, כי השלילה של פסוק זה היא
"אין זה נכון שX קטן או שווה לY"
אבל עדיף בהרבה לומר, "X גדול מY".
דוגמה מתמטית נוספת לכך היא:
אם ידוע שהמספר X קטן או שווה לY
אז השלילה של X קטן מY תהיה
X=Y. ולא חלילה X גדול מY.


 - לקראת נישואין וזוגיות
- לקראת נישואין וזוגיות